Cours Plan de Travail
Le cours en vidéo
Définitions des fonctions affines
Vidéo 1 – QCM n°1 : identifié – anonymes ;
QCM n°2 identifié – anonymes
Exercice 1 : Correction en pdf
Dire si les fonctions suivantes sont affines ou non :
\(~f(x) = \dfrac{1}{2}x+3~\) ; \(~g(x) = 1 – x~\) ; \(~f(x)=3x^2~\) ; \(~k(x)=\dfrac{2x+3}{5}~\); \(~l(x)=\dfrac{x}{2}~\)
Propriété des fonctions affines
Vidéo 2 : + QCM n°3 identifié – anonymes
Exercice 2 :
- Déterminer la fonction affine \(f\) qui vérifie \(f(3)=2\) et \(f(1)=-2\) Correction en pdf
- Déterminer la fonction affine \(f\) qui vérifie \(f(-1)=5\) et \(f(2)=1\) Correction en vidéo
Représentation graphique d’une fonction affine
Vidéo 3
QCM n°4 : Identifié – Anonymes et QCM n°5 : Identifié – Anonymes
Exercice 3 : correction en pdf
Représenter graphiquement la fonction affine \(f\) définie par \(f(x) = 2 x +3\) –
Exercice 4 : Correction en pdf
On considère les fonctions affines \(f\) et \(g\) définie sur \(\mathbb{R}\) par \(f(x) = x+2\) et \(g(x) = 3 x -2\)
On appelle \((d_1)\) la droite représentative de \(f\) et \((d_2)\) la droite représentative de \(g\)
- Déterminer les coordonnées du point d’intersection de \((d_1)\) et \((d_2)\)
- Déterminer les positions relatives de deux droites
Détermination graphique de \(a\) et \(b\)
Vidéo 4 : + QCM n°6 : Identifié – Anonymes
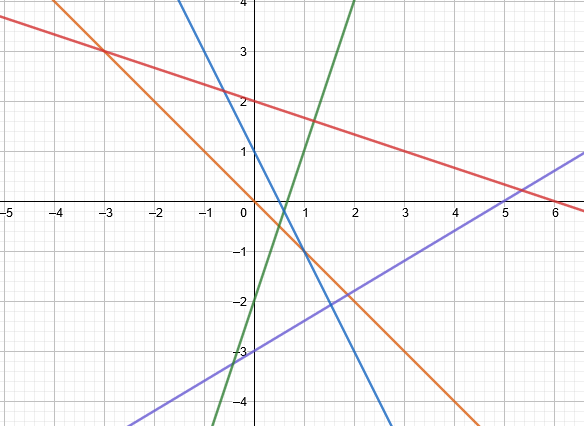Exercice 5 : Correction écrite
On considère les fonctions affines :
\(f_1\) représentée en rouge, \(f_2\) représentée en bleu ciel, \(f_3\) représentée en vert, \(f_4\) représentée en bleu marine et \(f_5\) représentée en orange dans le repère ci-dessous.
Déterminer les expressions de chacune de ces fonctions.
Fonction affine : sens de variation
Vidéo 5 : + QCM n°7 : Identifié – Anonymes
Exercice 6 : Correction en vidéo
Donner le sens de variation de la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x) = 2 x-3\) .
Exercice 7 : Correction en pdf
Donner le sens de variation de la fonction \(g\) définie sur \(\mathbb{R}\) par \(g(x) = 5-3 x\) .
Exercice 8 : Correction en pdf
Donner le sens de variation de la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x) = -2x+4\) puis le signe de \(f(x)\).
Exercice 9 : Correction en pdf
1. Donner le sens de variation de la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x) = -x+3\) puis tracer la représentation graphique de \(f\).
2. Peut-on comparer, sans calcul \(- \sqrt{2}+3\) et \(- \sqrt{3}+3\)
Exercice 10 : Correction en pdf
Donner le sens de variation des fonction \(f\) et \(g\) définies sur \(\mathbb{R}\) par \(f(x) = -x+2\) et \(g(x) = 2x\)
puis tracer leur représentation graphique dans le même repère.
Fonctions affines : signe d’une fonction affine
Vidéo 6 – Vidéo 7
QCM 8 : Identifié – Anonyme
Exercice 11 : Correction en vidéo
Déterminer le signe de la fonction \(g\) définie sur \(\mathbb{R}\) par \(g( x )=4-3x\)
Exercice 12 : Correction en vidéo
Déterminer le signe de la fonction \(v\) définie sur \(\mathbb{R}\) par \(v( x )=(1- \sqrt2) x + \sqrt3\)
Exercice 13 : Correction écrite
Déterminer le signe de la fonction \f\) définie sur \(\mathbb{R}\) par \(f(x) = – 2 x + 5\)
Résoudre une inéquation avec un tableau de signes
Résoudre dans \(\mathbb{R}\) : \((4x+1)(3-x)\geq 0\) : Vidéo 8 –
Exercice 14 :
Résoudre dans \(\mathbb{R}\) : \(( 5 x-1)(-2 x+1)> 0\) Correction écrite
Étude du signe d’une expression avec un tableau de signe
Vidéo 9 –
Exercice 15 : Correction écrite
Résoudre dans \(\mathbb{R}\) les inéquations suivantes :
\((3x-2)^2-(x+1)^2\geq 0\)