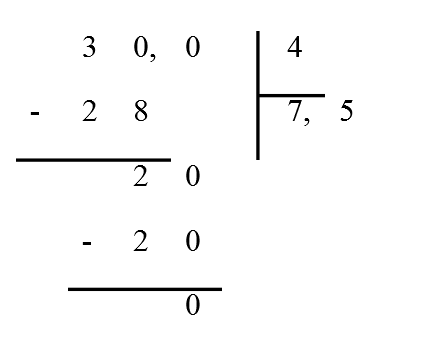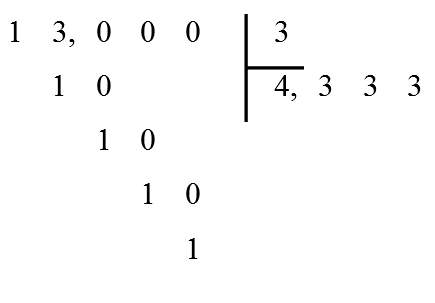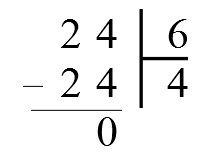1. Sens de l’écriture décimale :
1.1. Définitions
\(\bullet\) Quotient :
on appelle quotient de \(a\) par \(b\) le nombre qui multiplié par \(b\) donne \(a\) .}
\(\bullet\) Exemples :
\(\diamond\) Le quotient de 10 par 5 est le nombre qui multiplié par 5 donne 10 :
C’est à dire : \(5 \times \dots = 10\)
On trouve 2.
\(\diamond\) Le quotient de 2 par 5 est le nombre qui multiplié par 5 donne 2:
\(5 \times \dots = 2\)
C’est moins évident !
On trouve 0,4 donc le quotient de 2 par 5 vaut 0,4
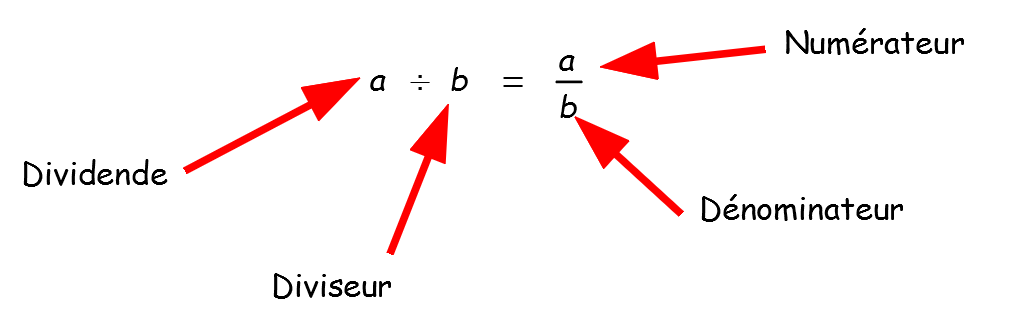
\(\bullet\) Fraction :
Dans le cas où \(a\) et \(b\) sont des nombres entiers, on dit que \(\frac{a}{b}\) est une fraction.
\(\bullet\) Exemples :
\(\frac{3}{5}\) ;\(\frac{21}{8}\) ;\(\frac{12}{11}\) sont des fractions.
\(\frac{12,24}{0,4}\) n’est pas une fraction car le numérateur et le dénominateur ne sont pas des entiers.
1.2. Différents quotients :
\(\bullet\) Le quotient est un nombre entier :
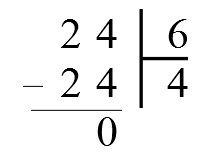
On trouve : \(\frac{24}{6}=4\). 4 est un nombre entier.
\(\bullet\) Le quotient est un nombre décimal :
Exemple :
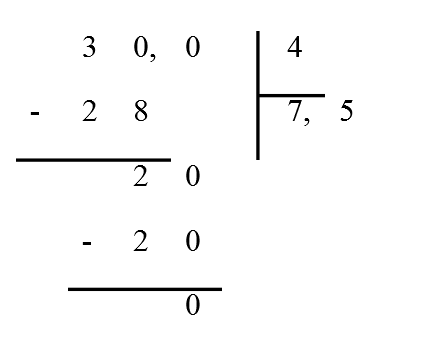
On trouve : \(\frac{30}{4}=7,5\). 7,5 est un nombre décimal.
\(\bullet\) Le quotient n’est pas un nombre décimal :
Exemple :
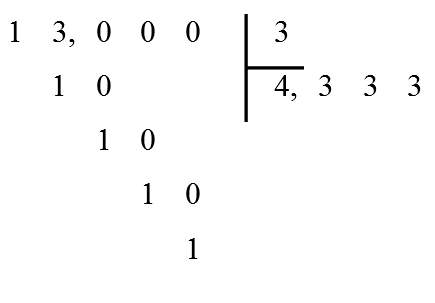
On trouve : \(\frac{13}{3}\approx 4,333\). La division ne se « termine » pas.
\(\frac{13}{3}\) n’est pas un nombre décimal.
Conclusion : Tous les quotients ne sont pas des nombres décimaux.
Par contre, on peut écrire n’importe quel nombre décimal en écriture fractionnaire.