Les fondamentaux pour le Bac :
Exercice 1 :
En suivant la loi uniforme, on choisit un nombre au hasard dans l’intervalle [4 ;11]. La probabilité que ce nombre soit inférieur à 10 est :
a) $$\dfrac{6}{11}$$ b) $$\dfrac{10}{7}$$ c) $$\dfrac{10}{11}$$ d) $$\dfrac{6}{7}$$
Exercice 2 :
On choisit au hasard un nombre réel dans l’intervalle [10;50]. La probabilité que ce nombre appartienne à l’intervalle [15; 20] est :
a) $$\dfrac{5}{50}$$ b) $$\dfrac{1}{8}$$ c) $$\dfrac{1}{40}$$ d) $$\dfrac{1}{5}$$
Exercice 3 :
$$X$$ est une variable aléatoire qui suit la loi normale de moyenne 3 et d’écart-type 2 alors une valeur approchée au centième de la probabilité $$p(X\geqslant5)$$ est
a) 0,14 b) 0,16 c) 0,32 d) 0,84
Exercice 4 :
La variable aléatoire $$X$$ suit une loi normale d’espérance $$\mu=0$$ et d’écart type $$\sigma$$ inconnu mais on sait que $$P(-10 \leqslant X \leqslant 10)=0,8$$.
On peut en déduire :
a) $$ P(X\leqslant10)=0,1$$ b) $$ P(X\leqslant10)=0,2 $$
c) $$ P(X\leqslant10)=0,5$$ d) $$P(X\leqslant10)=0,9$$
Exercice 5 :
Une variable aléatoire $$X$$ suit la loi uniforme sur l’intervalle [0; 5] dont la fonction de densité est représentée ci-dessous. Déterminer la bonne égalité :
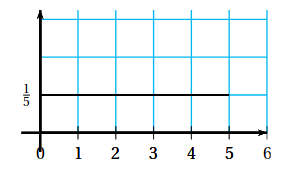
a) $$P(X\geqslant3)=P(X\leqslant3)$$ b) $$P(1\leqslant X \leqslant 4)=\dfrac{1}{3}$$
c) $$E(X)=\dfrac{5}{2}$$ d) $$E(X)=\dfrac{1}{5}$$
Exercice 6 :
On modélise le nombre de parties jouées par jour à une loterie par une variable aléatoire $$X$$ qui suit une loi normale d’espérance $$\mu=150$$ et d’écart-type $$\sigma=10$$.
Une valeur approchée à $$10^{-3}$$ près de $$P(140 \leqslant X \leqslant 160)$$ est
a) 0,954 b) 0,683 c) 0,997 d) 0,841
Exercice 7 :
Cette épreuve permet de développer sa VMA (vitesse maximale aérobie) qui correspond à une vitesse de course rapide. L’unité de mesure de la VMA est le km/h.On choisit un élève au hasard parmi les 120 élèves.
On admet que la VMA d’un élève pris au hasard est modélisée par une variable aléatoire $$Y$$ qui suit la loi normale d’espérance $$\mu=11,8$$ et d’écart type $$\sigma=1,2$$.
- Quelle est la probabilité arrondie à $$10^{-3}$$ , qu’un élève de terminale de ce lycée ait une VMA comprise entre 10 et 13 km/h?
- Déterminer la valeur arrondie au dixième de $$\alpha$$ tel que $$P(Y \leqslant \alpha)=0,8$$. Interpréter cette valeur dans le contexte de l’exercice.