Exercice 15 :

Résoudre dans \(\mathbb{R}\) les inéquations suivantes :

\((3x-2)^2-(x+1)^2\geq 0\)

Pour étudier le signe de cette expression, il faut la transformer en produit, pour se ramener à un tableau de signes.

Pour factoriser, on pense à la 3ème identité remarquable \(a^2-b^2=(a-b)(a+b)\)

Il vient donc :

\((3x-2)^2-(x+1)^2\geq 0\)

\(\iff \left(3x-2-(x+1)\right)\left(3x-2+(x+1)\right)\geq 0\)

\(\iff \left(3x-2-x-1\right)\left(3x-2+x+1\right)\geq 0\)

\(\iff \left(2x-3\right)\left(4x-1\right)\geq 0\)

On reconnaît le produit de deux fonctions affines \(f\) et \(g\) définies sur \(\mathbb{R}\)

par \(f(x)=2x-3\) et \(g(x)=\)

Pour \(f\) : \(a=2>0\) et \(\dfrac{-b}{a}= – \dfrac{-3}{2}=\dfrac{3}{2}\)

Pour \(g\) : \(a=4>0\) et \(\dfrac{-b}{a}= – \dfrac{-1}{4}=\dfrac{1}{4}\)

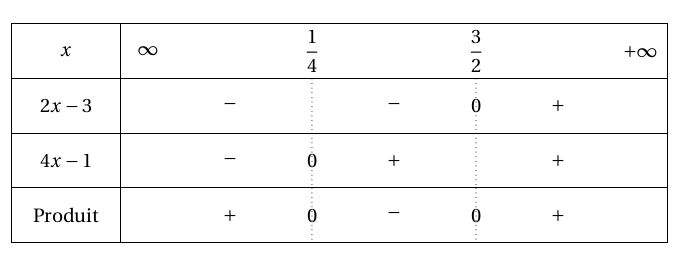
On trouve alors : \(S=]-\infty;\dfrac{1}{4}]\cup [\dfrac{3}{2};+\infty[\)