Cette partie est en construction, elle est donc pour le moment incomplète.
Calculer : $A=\dfrac{8}{9}-\dfrac{2}{9} \times \dfrac{7}{3}\quad\quad$ puis $ B=3-\dfrac{9}{15} \times \dfrac{5}{12}\quad\quad$
Calculer : $A=\dfrac{3}{4}+\dfrac{5}{4} \div\left(\dfrac{1}{2}-\dfrac{4}{3}\right)\quad\quad\quad$
Exercice 1 :Simplifier l'écriture de : $-\sqrt{5}(4-\sqrt 5)$ puis de $ (\sqrt 6 +1)(5-2\sqrt6)\quad\quad\quad$
CorrectionExercice 2 :Simplifier l'écriture de : $\sqrt{2}(2-3\sqrt 2)\quad\quad\quad$
Correction en vidéo Exercice 3 :Simplifier l'écriture de : $(3\sqrt{2}+5)(\sqrt 2-3)\quad\quad\quad$
Correction en vidéo Exercice 4 :Simplifier l'écriture de : $(4+5\sqrt{2})(2-3\sqrt 2)\quad\quad\quad$
Correction en vidéo Exercice 5 :Simplifier l'écriture de : $(5+\sqrt 2)^{2}~~;~~(3-2\sqrt 5)^{2}~~;~~(2-\sqrt 3)(2+\sqrt 3)\quad\quad\quad$
Correction Haut de page
Le cours en ligne et en vidéoIV
Développer et factoriser :
A
Développer une expression :
Développer : $6 x(7 x-5)+7 x\quad$
CorrectionExercice 2 :Développer et réduire :
$D = (4x + 7) (8 -x) + (5x + 6) (7 - 2x)\quad$
Aide pour démarrer$\quad$
CorrectionExercice 3 :Développer et réduire :
$E = (x+3) (9x+2) - (3x+5) (1 - 2x)$
Aide pour démarrer$\quad$
CorrectionExercice 4 :Développer et réduire : $E = (4x-1) (2x+3) - (1-2x) (5x+7)$
CorrectionExercice 5 :Développer et réduire : $A=(7 x-4)^{2}-(5 x-1)(3-2 x)$
CorrectionExercice 6 :Développer et réduire : $A=(4 x+5)^{2}-(2 x+3)(2 x-3)$
CorrectionHaut de pageB
Factoriser une expression :
Exercice 1 :
Factoriser, si possible :
$A=x^{2}+2 x+1 $
$ B=4 x^{2}+12 x+9$
$C=9 x^{2}-24 x+16 $
$ D=49 x^{2}-42 x+36\quad$
CorrectionExercice 2 :Factoriser :
$A=x^{2}-4 \quad ; \quad B=25 x^{2}-1$
Correction Exercice 3 :Factoriser $B=16-(4-x)^{2}$
CorrectionExercice 4 :Factoriser $C=(1+2 x)^{2}-(3 x-1)^{2}$
CorrectionExercice 5 :Factoriser A = $36-(2x+4)^2$
CorrectionFactoriser A = $(2a-1)^2-(3a + 2)^2$
Correction Haut de pageV
Résoudre des équations :
A
Résoudre des équations du premier degré :
Exercice 1 :Résoudre dans $\mathbb R$ : $2 x+4=12\quad\quad$
CorrectionExercice 2 :Résoudre dans $\mathbb R$ : $-2 x=-11\quad\quad$
CorrectionExercice 3 :Résoudre dans $\mathbb R$ : $3 x-5=10\quad\quad$
CorrectionExercice 4 :
Résoudre dans $\mathbb R$ : $9(x-1)=11(x+4)\quad\quad$
Correction Exercice 5 :Résoudre dans $\mathbb R$ : $4(2-x)+4=-3 x+1\quad\quad$
CorrectionExercice 6 :
Résoudre dans $\mathbb R$ : $\dfrac{-2}{3} x=\dfrac{5}{7}\quad\quad\quad\quad\quad$
CorrectionExercice 7 :
Résoudre dans $\mathbb R$: $3(4+2 x)+7=7 x-5\quad\quad$
CorrectionExercice 8 :
Résoudre dans $\mathbb R$ : $-3 x-9=x-1\quad\quad\quad\quad$
CorrectionExercice 9 :
Résoudre dans $\mathbb R$ : $2 x-\dfrac{1}{4}=-3 x+\dfrac{2}{7}\quad\quad\quad$
Correction B
Résoudre des équations produit-nul ou s'y ramenant
Exercice 1 :Résoudre dans $\mathbb R$ : $(2 x+1)(5 x-8)=0\quad\quad\quad$
CorrectionExercice 2 :Résoudre dans $\mathbb R$ : $(2 x-3)^{2}-(7-4 x)^{2}=0\quad\quad$
CorrectionExercice 3 :Résoudre dans $\mathbb R$ :$(x-5)(x+7)-(2 x-8)(x+7)=0\quad\quad$
CorrectionExercice 4 :Résoudre dans $\mathbb{R}$ : $x^{2}-16=0\quad\quad\quad$
CorrectionExercice 5 :Résoudre dans $\mathbb{R}$ : $27 x^{2}-15 x=0\quad\quad\quad$
Correction Exercice 6 :Résoudre dans $\mathbb{R}$ : $x^{2}+25=0\quad\quad\quad$
CorrectionExercice 7 :Résoudre dans $\mathbb{R}$ : $(x-7)^{2}-11=0\quad\quad$
CorrectionExercice 8 :Résoudre dans $\mathbb{R}$ : $x^{2}-13=0\quad\quad\quad$
CorrectionExercice 9 :Resoudre dans $\mathbb R$ : $\quad(x-3) \times(2 x-4)=(2 x-4) \times(3 x+7)\quad\quad\quad\quad\quad$
Correction Exercice 10 :Resoudre dans $\mathbb R$ : $\quad \dfrac{3 x-5}{2 x-1}=0\quad\quad$
Correction Exercice 11 :Résoudre dans $\mathbb{R}$ : $(2 x+3)(4-x)-(2 x+3)^{2}=0\quad\quad$
Correction Haut de pageVI
Généralités sur les fonctions :
Lire l'image de $-2$ par la fonction représentée ci-dessous :
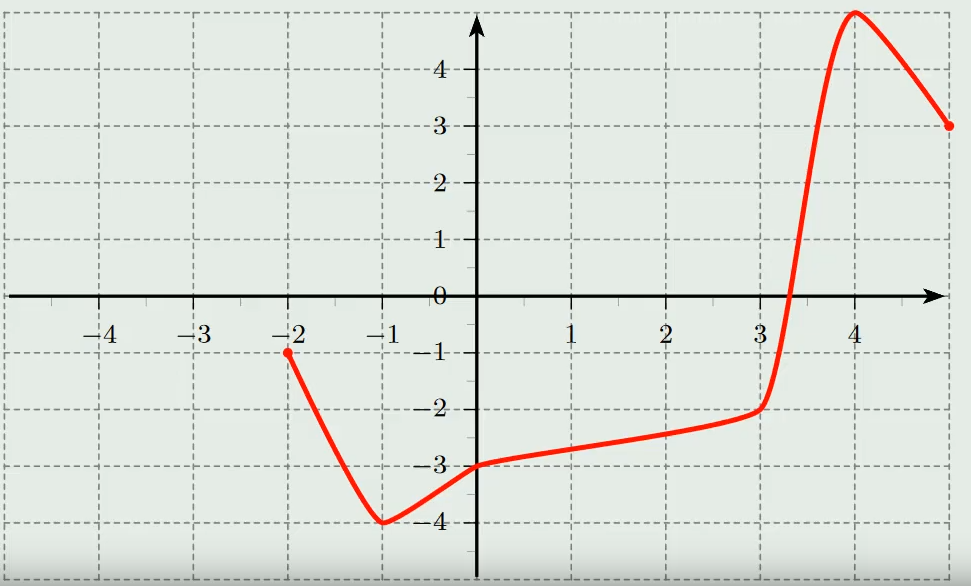 CorrectionExercice 2 :
CorrectionExercice 2 :Déterminer graphiquement l'ensemble de définition de la fonction $f$ représentée ci-dessous :
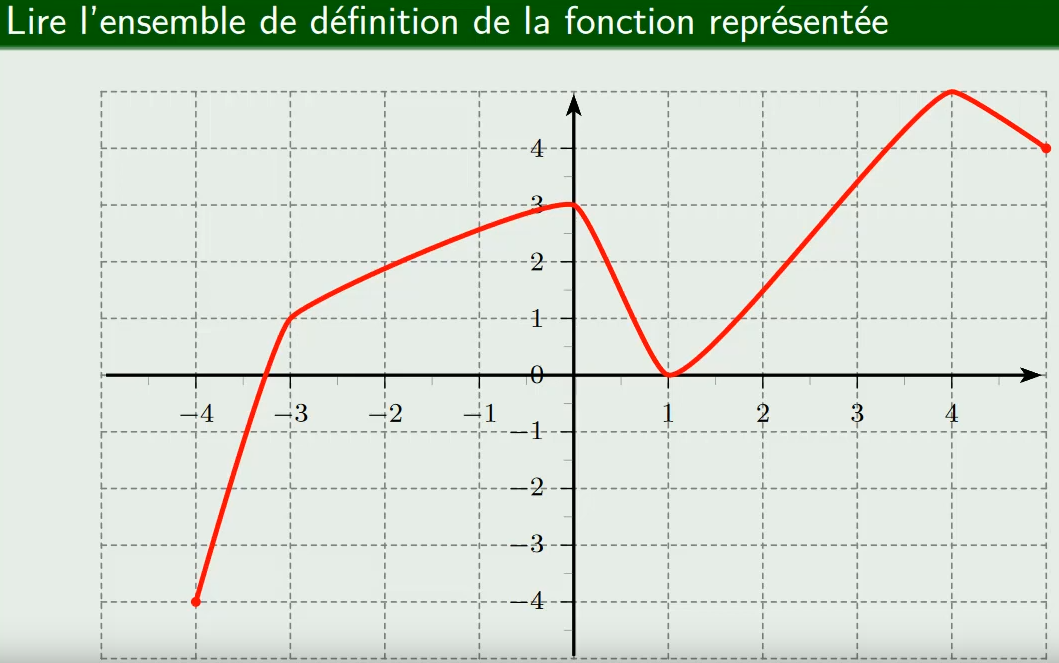 CorrectionExercice 3 :
CorrectionExercice 3 :Déterminer graphiquement l'ensemble de définition de la fonction $f$ représentée ci-dessous :
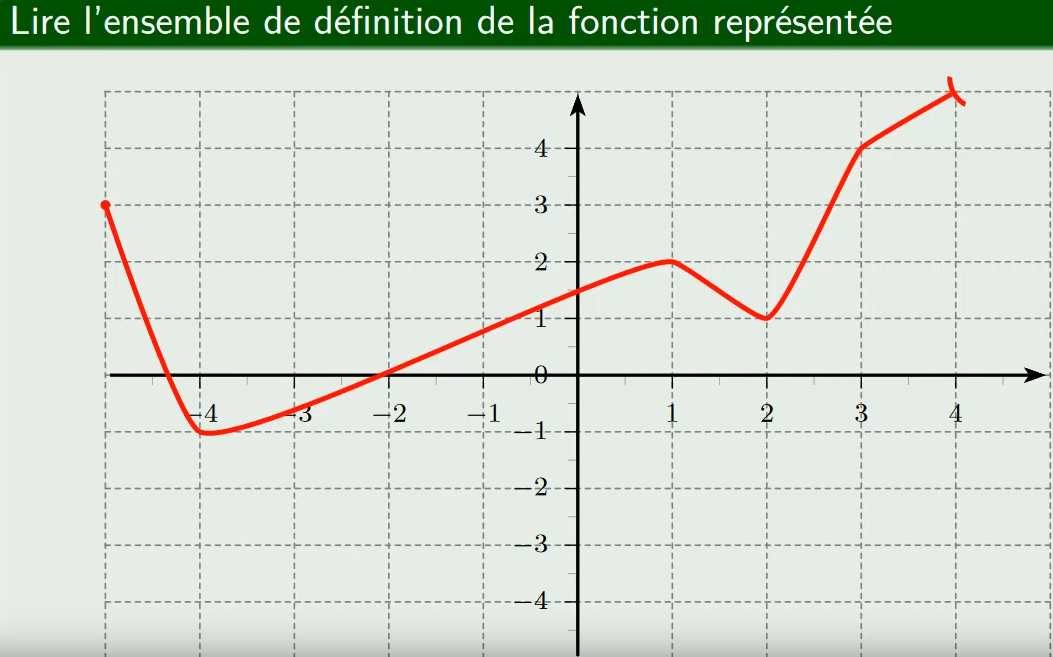 CorrectionExercice 4 :
CorrectionExercice 4 :
Résoudre graphiquement $f(x)=1$ à partir de la représentation graphique de la fonction $f$ ci-dessous :
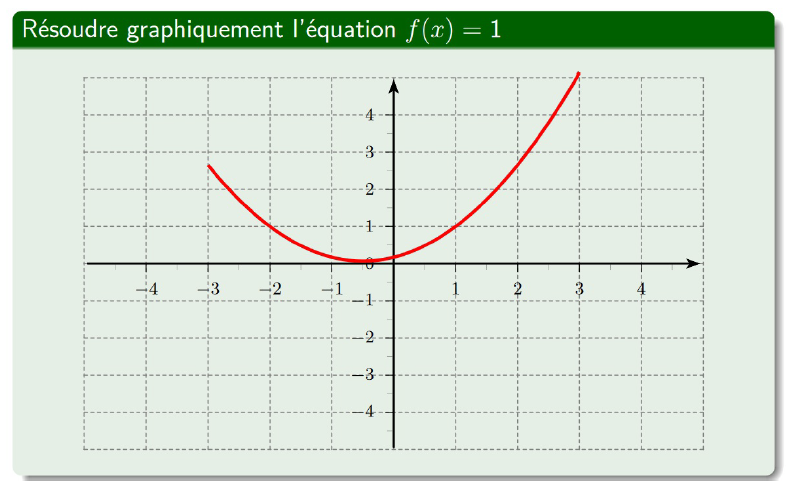 CorrectionExercice 5 :
CorrectionExercice 5 :
Résoudre graphiquement $f(x)\geq-3$ à partir de la représentation graphique de la fonction $f$ ci-dessous :
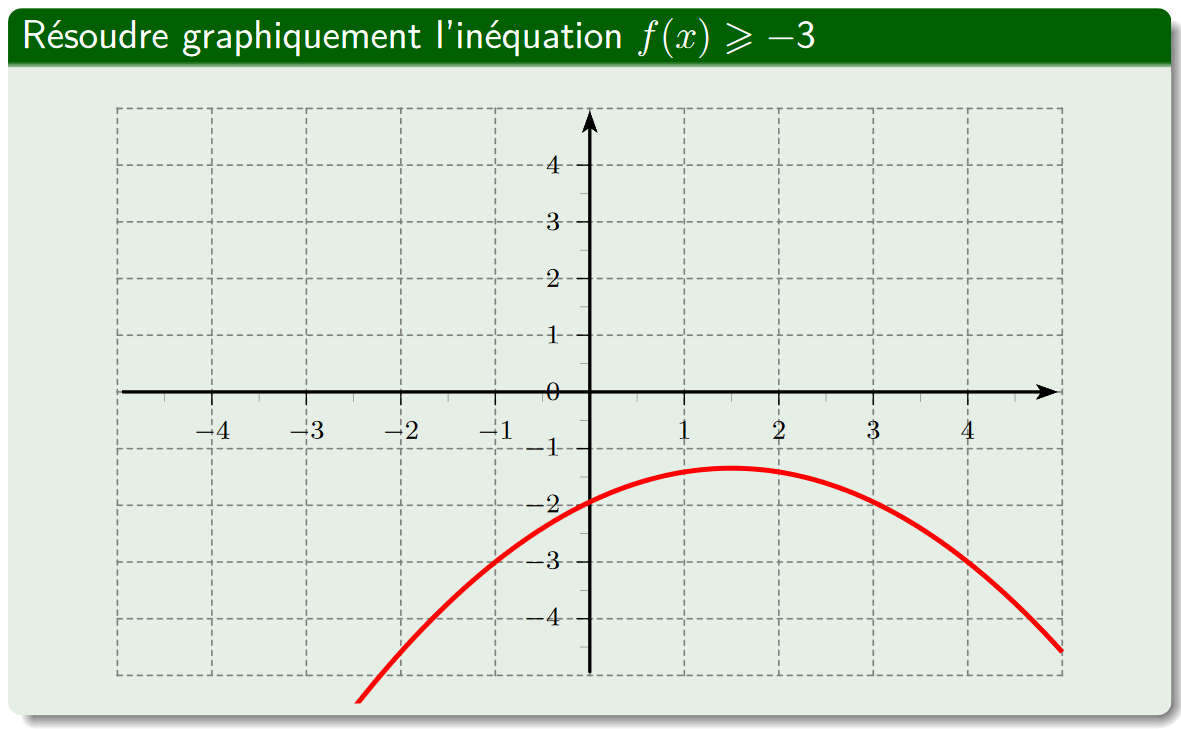 CorrectionExercice 6 :
CorrectionExercice 6 :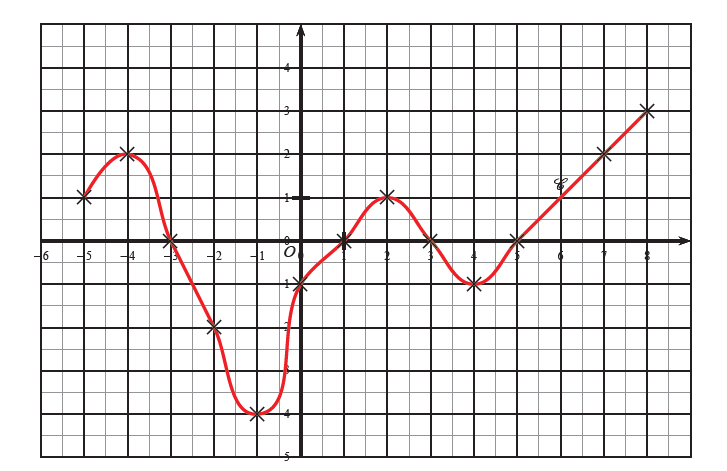 Partie A : Correction
Partie A : Correction1. Quel est l'ensemble de définition $\mathcal{D}$ de $f$ ?
2. Quelle est l'image de $2$ par la fonction $f$ ?
3. Combien vaut $f(4)$ ?
4. Donner le ou les antécédents de $2$ par la fonction $f$ ?
5. Déterminer une image ayant un seul antécédent.
6. Quel est le nombre maximum d'antécédents que peut avoir une image sur cet intervalle ? Donner un exemple.
Partie B : Correction1. Résoudre graphiquement, en rédigeant votre réponse, l' équation : $f(x)=3$
2. Sans justifier, donner les solutions des équations suivantes : $f(x)=0$ et $f(x)=4$
3. Résoudre graphiquement, en justifiant votre réponse, l' inéquation suivante :$f(x)<0$
4. Sans justifier, donner les solutions de l'inéquation suivante :$f(x)\leqslant 2$
Correction complète Exercices 6 et 7 en pdfHaut de pageExercice 7 :Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=-2x^{2}-3x+1$.
1. Calculer l'image de $-1$
2. Calculer $f(\sqrt 2)$
3. Quels sont les antécédents $1$ par $f$?
4. Le point de coordonnées $(1;-5)$ appartient-t-il à la courbe représentative de $f$ ?
Correction Correction complète Exercices 6 et 7 en pdfVII
Variations de fonctions
$f$ est une fonction définie sur l'intervalle [-7 ; 8], on donne son tableau de variations :
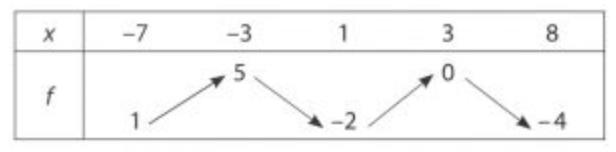
Compléter avec "< "ou ">" en expliquant :
a. $ f(-6) ...... f(-4)$
Correction b. $ f(-2) ...... f(-1)$
Correction c. $ f(4) ...... f(5)$
Correction d. $ f(-4) ...... f(2)$
Aide pour démarrer Correction 2. Quel est le maximum de cette fonction sur [-7 ; 8] ?
Correction Exercice 2 :La fonction $f$ est décroissante sur $]-\infty ;-1]$ et sur $[3 ;+\infty[$ et croissante sur $[-1 ; 3]$ .
On sait d'autre part que $f(-4)=f(3)$ et $f(5)=f(-1)$
1. Peut-on comparer
$\quad$ a. $\quad f(4)$ et $f(-4)=f(3)$ ?
$\quad$ b. $f(-3)$ et $f(-1)$ ?
$\quad$ c. $f(4)$ et $f(2)$ ?
$\quad$ d. $f(-4)$ et $f(5)$ ?
Correction 1.a.b.c.d. 2. Pour $x \in[-1 ; 7],$ comparer $f(x)$ et $f(3)$
3. Pour $x \in]-\infty ; 5],$ comparer $f(x)$ et $f(-1)$
Correction 2 et 3 Exercice 3 :Voici un tableau de variations incomplet :
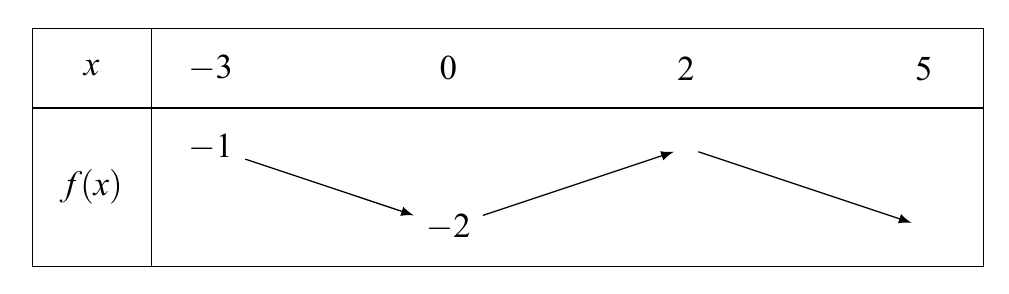
1. Compléter si possible ce tableau sachant que :
$\quad\bullet\quad$ le minimum de $g$ est -3 ,
$\quad\bullet\quad$ le maximum de $g$ est -1 .
2. Décrire le sens de variations de $g$ par des phrases.
3. $\quad$ a. Alain affirme que $g(-1)=-2,1$. Est-ce plausible?
$\quad$ b. Aline affirme que $- 2$ admet exactement deux antécédents. Est-ce plausible ?
$\quad$ c. Encadrer $g(2)$ le plus précisément possible.
$\quad$ d. Résoudre l'inéquation $g(x)>-3$.
Haut de page
Haut de page
A
Reconnaître une fonction affine :
Parmi les fonctions suivantes, lesquelles sont affines ?
$f \text{ définie sur} ~~\mathbb R ~~\text{par}\quad f(x)=3x-4 \quad\quad\quad\quad\quad g \text{ définie sur} ~~\mathbb R ~~\text{par}\quad g(x)=6-2x$
$h \text{ définie sur} ~~\mathbb R ~~\text{par}\quad h(x)=-x\quad\quad\quad\quad\quad\quad\ i \text{ définie sur} ~~\mathbb R ~~\text{par}\quad i(x)=2x^2-3$
$j \text{ définie sur} ~~\mathbb R ~~\text{par}\quad j(x)=-\dfrac{2}{x}-4 \quad\quad\quad\quad\quad k \text{ définie sur} ~~\mathbb R ~~\text{par}\quad k(x)=\pi x - \sqrt 2$
$l \text{ définie sur} ~~\mathbb R ~~\text{par}\quad l(x)=-3$
Correction B
Déterminer une fonction affine :
Déterminer la fonction affine $f$ qui vérifie $f(-1)=5$ et $f(2)=1$
Correction Exercice 3 :Déterminer la fonction affine vérifiant : $f(3)=4$ et $f(5)=7$
Correction C
Lire graphiquement $a$ et $b$ :
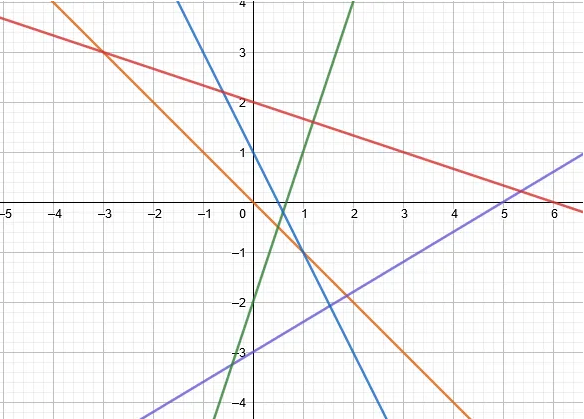
On considère les fonctions affines :
$f_1$ représentée en rouge, $f_2$ représentée en bleu ciel, $f_3$ représentée en vert, $f_4$ représentée en bleu marine et $f_5$ représentée en orange dans le repère ci-dessous.
Déterminer les expressions de chacune de ces fonctions.
Correction D
Représenter une Fonction Affine :
Représenter graphiquement la fonction $f$ définie sur $\mathbb R$ par $f(x)=3x-4$
Correction E
Déterminer le sens de variation d'une fonction affine :
Donner le sens de variation de la fonction $f$ définie sur $\mathbb{R}$ par $f(x) = 2 x-3$. .
Correction Exercice 7 : Donner le sens de variation de la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=3x-7$
Correction F
Déterminer le signe d'une fonction affine :
Déterminer le signe de la fonction $g$ définie sur $\mathbb{R}$ par $g( x )=4-3x$
Correction Exercice 9 : Déterminer le signe de la fonction $v$ définie sur $\mathbb{R}$ par $v( x )=(1- \sqrt2) x + \sqrt3$
Correction Exercice 10 : Déterminer le signe de la fonction $f$ définie sur $\mathbb{R}$ par$f(x)=-0,4 x+2$
Correction G
Résoudre une inéquation produit :
Résoudre dans $\mathbb R$ : $(2-3x)(4x+3)<0$
Enoncé et Correction H
Etude du signe d'une expression complexe :
Etudier le signe sur $\mathbb R$ de l'expression :$A(x)=(3 x -1)^2- (2 x+7)^2$
Enoncé et CorrectionHaut de page

















