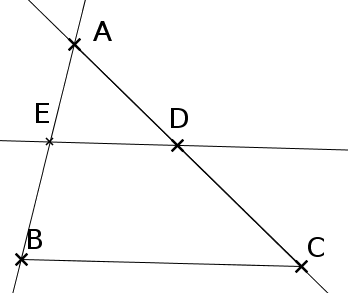
Soit la configuration suivante.
On donne AD=3 cm, AC=5 cm, AE=4cm et BC=4cm.
Calculer AB et ED.
On sait que : - D appartient à (AC)
- E appartient à (AB)
-(ED) et (BC) sont parallèles.
D’après le théorème de Thalès :
${AD\over AC} = {AE \over AB}={ED \over BC}$
${3\over 5} = {4 \over AB}={ED \over 4}$
D’où en utilisant l’égalité des produits en croix,(voir chapitre fraction et quotient) on a :
$3 \times AB=4 \times 5$
$3 \times AB=20$
$ AB={20 \over 3}$
| $3 \times 4=5 \times ED$
$12=5 \times ED$
$ ED={12 \over 5}=2,4$
|
On aurait pu écrire directement
$ AB={4\times 5 \over 3}={20 \over 3}$ $ ED={3\times 4 \over 5}=2,4$
Retour à la page de cours









