Le cours en pdf
Lien vers mathsguyon.frI
Limites finies à l'infini
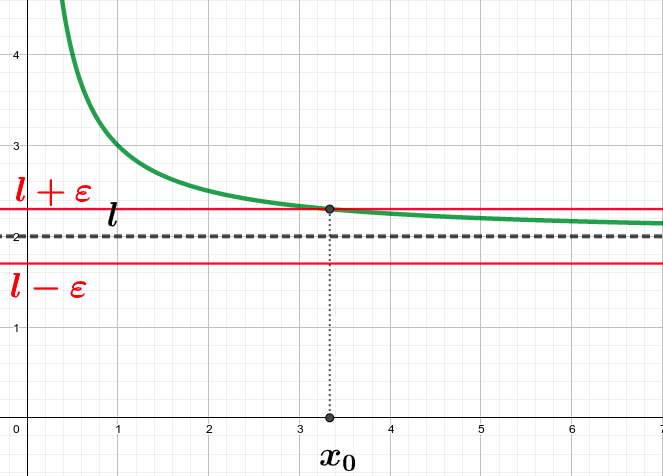
Déplacez le curseur rouge de l'animation Géogébra ci-dessous :
On observe que la courbe représentative de la fonction se rapproche d'une droite horizontale quand les valeurs des antécédents augmentent.
On peut moduler l'intervalle autour de la valeur $l$, on trouvera toujours un $x$ suffisamment grand, pour que les antécédents supéreiurs donnent des images dans l'intervalle coloré.
Comprendre :
Dire qu'une fonction admet une limite $l$ quand $x$ tend vers $+\infty$ signifie qu'à partir d'une certaine valeur $x_0$ pour les antécédents, toutes les images seront proches de $l$.
Graphiquement, cela signifie que :
Faîtes bouger le curseur $\lambda$ en bas de page, pour moduler l'intervalle autour de la valeur limite $l$.
Une fois le curseur positionné, vous pouvez déplacer la droite verte, et trouver la valeur de $x_0$ à partir de laquelle toutes les images seront dans votre intervalle.
B
Définition et première propriété :
Comprendre :
Soit $f$ une fonction définie sur un intervale $I$. Soit $l\in\mathbb R$.
On dit que la fonction $f$ admet pour limite $l$ lorsque $x$ tend vers $+\infty$
si $f(x)$ prend des valeurs aussi proches de $l$ que l'on souhaite pourvu qu'on prenne des $x$ assez grand.
On note : $\lim\limits _{x \rightarrow +\infty} f(x)=l$
On dit aussi que $f(x)$ tend vers $l$ quand $x$ tend vers $+\infty$ .
Remarque 1 :
On peut avoir le même phénomène quand $x$ tend vers $-\infty$ et avoir $\lim\limits _{x \rightarrow -\infty} f(x)=l$
Définition 1 :
Cette définition rigoureuse est sans doute hors programme, mais elle exprime de manière précise la notion abordée.Soit $f$ une fonction définie sur un intervalle $[a ;+\infty[$ où $a \in \mathbb{R} .$
Soit $l$ un réel. $f$ admet pour limite $l$ en $+\infty$ si :
Pour tout intervalle I tel que $l\in I$, il existe un réel $x_{0}$ tel que pour tous les réels $x>x_{0}$ , $f(x) \in I$
Définition 2 :
On peut rédiger cette définition en langage mathématique, ce qui est clairement hors programme mais pas inintéressant pour ceux qui poursuivront les maths.$$\lim\limits_{x \rightarrow+\infty} f(x)=l \iff \forall \epsilon>0, \exists x_0\in\mathbb R, \forall x>x_0, \vert f(x)-l\vert <\epsilon$$
Propriété 1 :
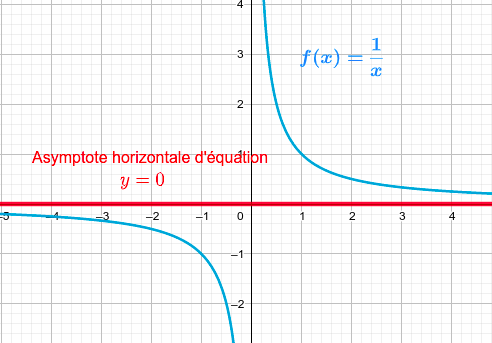
Limites finies de fonctions de références : $\quad\bullet\quad$$\lim\limits _{x \rightarrow+\infty} \dfrac{1}{x}=0\quad\quad\quad\bullet\quad$ $\lim\limits _{x \rightarrow-\infty} \dfrac{1}{x}=0$
Définition 1 :
Soit $l \in \mathbb{R}$ et soit $\mathcal{C}$ la courbe représentative d'une fonction $f$ dans un repère.
On dit que la droite d'équation $y=l$ est
asymptote horizontale à la courbe $\mathcal{C}$ :
$\quad\bullet\quad$ en $+\infty$, si $\lim\limits _{x \rightarrow+\infty} f(x)=l$
$\quad\bullet\quad$ en $-\infty$, si $\lim\limits _{x \rightarrow-\infty} f(x)=l$
Exemple 1 :
D'après la propriété vu précédemment, on sait que :
$\lim\limits _{x \rightarrow+\infty} \dfrac{1}{x}=0$ et $\lim\limits _{x \rightarrow-\infty} \dfrac{1}{x}=0$
donc la droite d'équation $y=0$ est une asymptote horizontale à l'hyperbole en $+\infty$ et en $-\infty$.
II
Limites infinies à l'infini
Définition 1 :
$f$ admet pour limite $+\infty$ en $+\infty$ si pour tout intervalle $] M ;+\infty[$ où $M$ est un réel,
il existe un réel $x_{0}$ tel que pour tous les réels $x$ supérieurs à $\left.x_{0}, f(x) \in\right] M ;+\infty[$
On note alors $\lim\limits _{x \rightarrow+\infty} f(x)=+\infty$
On dit aussi que $f(x)$ tend vers $+\infty$ quand $x$ tend vers $+\infty$.
Définition 2 :
$f$ admet pour limite $-\infty$ en $+\infty$ si pour tout intervalle $]-\infty;M [$ où $M$ est un réel,
il existe un réel $x_{0}$ tel que pour tous les réels $x$ inférieurs à $x_{0}$, $f(x) \in ]-\infty;M[$
On note alors $\lim\limits _{x \rightarrow+\infty} f(x)=-\infty$
On dit aussi que $f(x)$ tend vers $-\infty$ quand $x$ tend vers $+\infty$.
Remarque 1 :
On définit de la même manière $\lim\limits _{x \rightarrow-\infty} f(x)$
Remarque 2 :
Limites et
monotonie ne sont, en général, pas liées.
On peut montrer que pour la fonction $f$ définie sur $\mathbb R$ par $f: x \mapsto x+\cos (x)$
on a $: \lim\limits _{x \rightarrow+\infty} f(x)=+\infty$
et $\lim\limits _{x \rightarrow-\infty} f(x)=-\infty$
mais que cette fonction n'est pourtant pas croissante.
On retient donc qu'une fonction peut tendre vers $+\infty$ sans être forcément croissante.
Propriété 1 :
Limites finies de fonctions de références : $ \bullet \lim\limits _{x \rightarrow+\infty} x=+\infty \quad\quad\quad \bullet \lim\limits _{x \rightarrow+\infty} x^{2}=+\infty\quad\quad\quad\bullet \lim\limits _{x \rightarrow+\infty} x^{3}=+\infty \quad\quad\quad\bullet \lim\limits _{x \rightarrow+\infty} \sqrt{x}=+\infty$
$ \bullet \lim\limits _{x \rightarrow-\infty} x=-\infty \quad\quad\quad \bullet \lim\limits _{x \rightarrow-\infty} x^{2}=+\infty\quad\quad\quad\bullet \lim\limits _{x \rightarrow-\infty} x^{3}=-\infty$
Propriété 2 :
D'une manière générale, on admet que, pour tout entier naturel $k\neq 0$ : : $ \lim\limits _{x \rightarrow+\infty} x^{k}=+\infty $
A
Extrémité finie d'un intervalle du domaine de définition :
On considère dans ce paragraphe une fonction $f$ définie sur un ensemble $D_{f}$
et $a \in D_{f}$ où $a$ est l'extrémité d'un intervalle de $D_{f}$.
Exemple 1 :
Soit $f$ la fonction définie sur $D_f=]-\infty;-2[\cup]3;+\infty[$.
D'après la consigne $a$ est une extrémité de $D_f$ donc dans ce cas-ci,
on peut avoir : $a=-2$ ou $a=3$, puisque $a$ est un nombre réel.
Comprendre :
L'idée de cette partie est d'analyser le comportement d'une fonction à proximité d'une valeur réelle, pour laquelle la fonction n'est pas définie.
On va donc étudier une limite quand $x$ va tendre vers cette valeur réelle, sans l'ateindre puisqu'elle est exclue du domaine de définition.
Pour reprendre la fonction précedente, définie sur $D_f=]-\infty;-2[\cup]3;+\infty[$,
on sera amenés à calculer la limite quand $x \rightarrow -2$ et quand $x \rightarrow 3 $,
pour étudier le comportement de la fonction "aux bornes" de son domaine de définition.
Comprendre :
Soit $f$ une fonction définie sur un intervale $I$; Soit $a\in \mathbb R$.
On dit que la fonction $f$ admet pour limite $+\infty$ lorsque $x$ tend vers $a$ si $f(x)$ prend des valeurs de plus en plus grandes pour des $x$ très proches de $a$.
On note : $\lim\limits _{x \rightarrow a} f(x)=+\infty$
Exemple 1 :
Dans cette situation, la fonction étudiée n'est pas définie en 1.
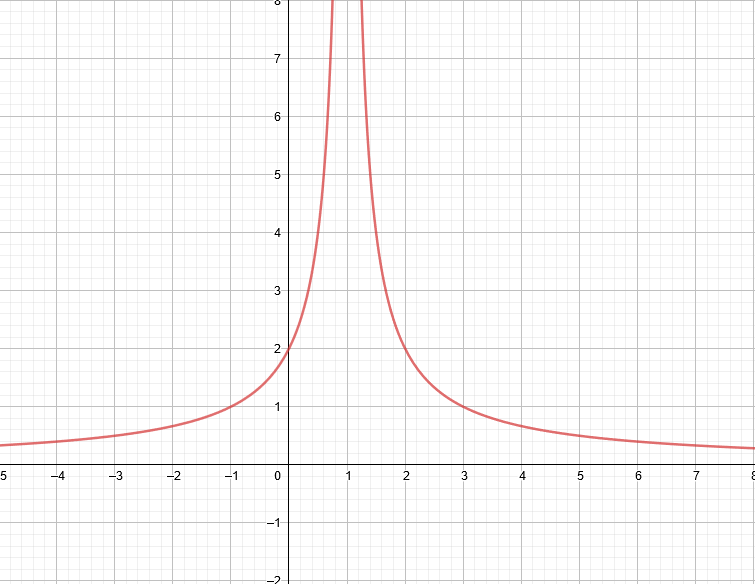
La fonction tend vers l'infini quand les antécédents se rapprochent de $1$.
On note : $\lim\limits _{x \rightarrow 1} f(x)=+\infty$
C
Limite "à gauche" et limite "à droite" :
Exemple 1 :
Dans cette situation, la fonction étudiée n'est pas définie en $-2$ et les limites "à gauche" et "à droite" sont différentes.
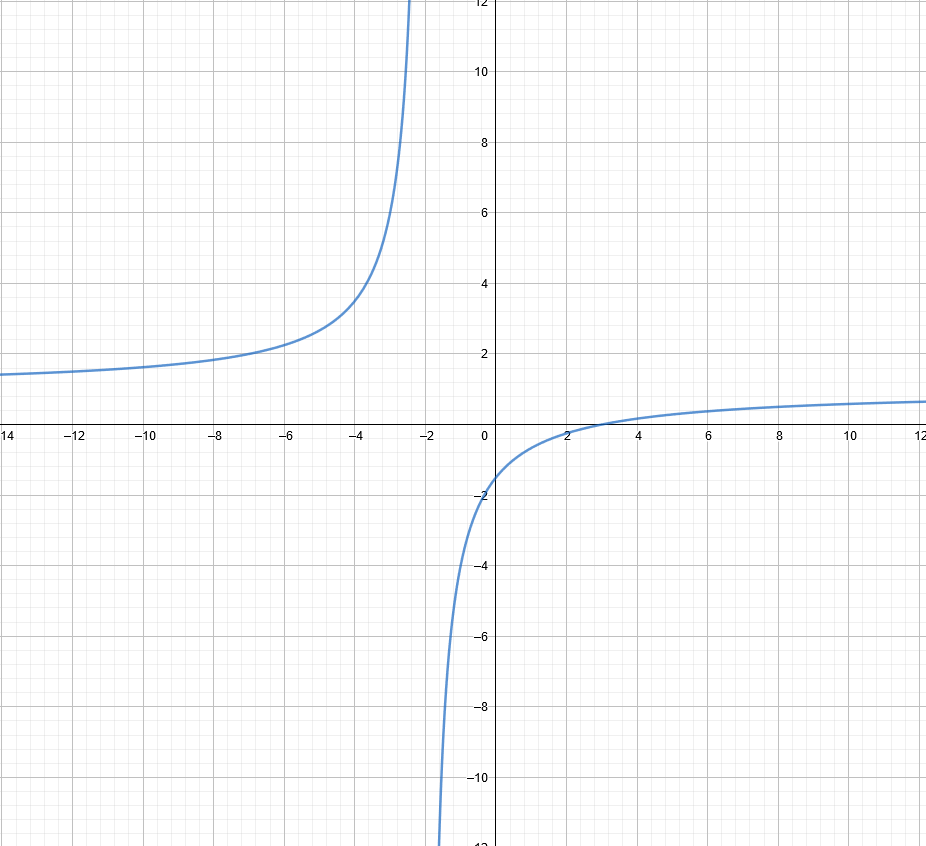
On comprend qu'il faut étudier une limite "à gauche" et une limite "à droite", puisqu'il y a deux branches distinctes.
Comprendre :
Dans cette situation, il est impossible de définir $\lim\limits _{x \rightarrow -2} f(x)$ .
Il faut distinguer la limite quand $x \rightarrow -2$ par valeur inférieure, et la limite quand $x \rightarrow -2$ par valeur supérieure.
On note alors :$\lim\limits _{\substack{x \rightarrow -2 \\ x>-2}}f(x)$ quand $x \rightarrow -2$ par valeur supérieure.
et $\lim\limits _{\substack{x \rightarrow -2 \\ x<-2}}f(x)$ quand $x \rightarrow -2$ par valeur inférieure.
On a alors dans cette situation :
$\lim\limits _{\substack{x \rightarrow -2 \\ x<-2}} f(x)=+\infty$ et $\lim\limits _{\substack{x \rightarrow -2 \\ x>-2}} f(x)=-\infty$
Définition 1 :
Soit $a$ un réel, $\mathcal{C}$ la courbe représentative d'une fonction $f$ dans un repère.
On dit que la droite d'équation $x=a$ est
asymptote verticale à $\mathcal{C}$ si la
limite à droite ou la limite à gauche de $f$ en $a$ est $+\infty$ ou $-\infty$.
Exemple 1 :
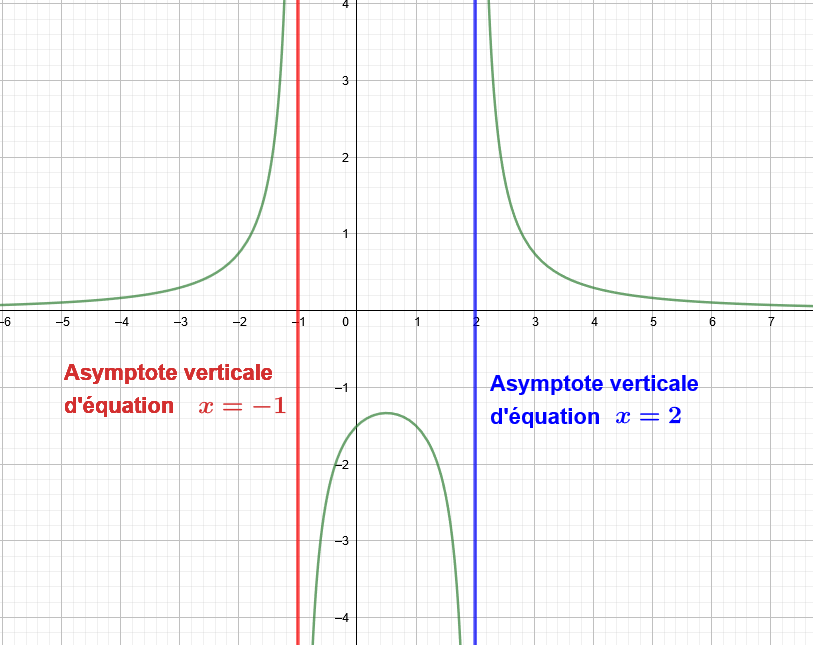
Dans cette situation, la fonction représentée admet deux asymptotes verticales,
d'équation $x=-1$ et $x=2$
IV
Opérations sur les limites
Propriété 1 :
On résume les résultats des limites de sommes de fonctions, où $a$ est un réel ou $a=+\infty$ ou $a=-\infty$ :

Propriété 1 :
On résume les résultats des limites de produits de fonctions, où $a$ est un réel ou $a=+\infty$ ou $a=-\infty$ :
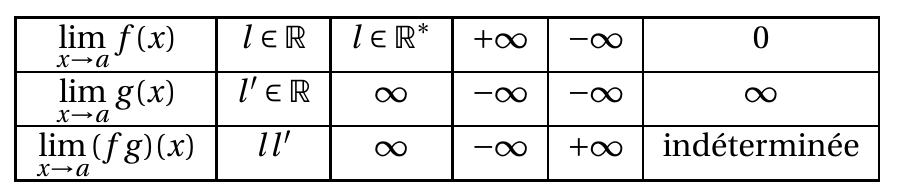
Propriété 1 :
On résume les résultats des limites de qutotients de fonctions, où $a$ est un réel ou $a=+\infty$ ou $a=-\infty$ :

Définition 1 :
Quand on obtient une limite nulle, il est souvent important de déterminer si
la fonction tend vers $0$ par valeurs positives ou par valeurs négatives.
Le signe a en effet un impact dans le tableau des quotients vu au dessus.
Exemple 1 :
$\quad\bullet\quad$ $\lim\limits _{\substack{x \rightarrow 2 \\ x>2}} x-2=0$ mais comme $x>2$, la limite sera positive.
On notera alors : $\lim\limits _{\substack{x \rightarrow 2 \\ x>2}} x-2=0^{+}$
$\quad\bullet\quad$ $\lim\limits _{\substack{x \rightarrow 2 \\ x<2}} x-2=0$ mais comme $x<2$, la limite sera négative.
On notera alors : $\lim\limits _{\substack{x \rightarrow 2 \\ x<2}} x-2=0^{-}$
Exemple 2 :
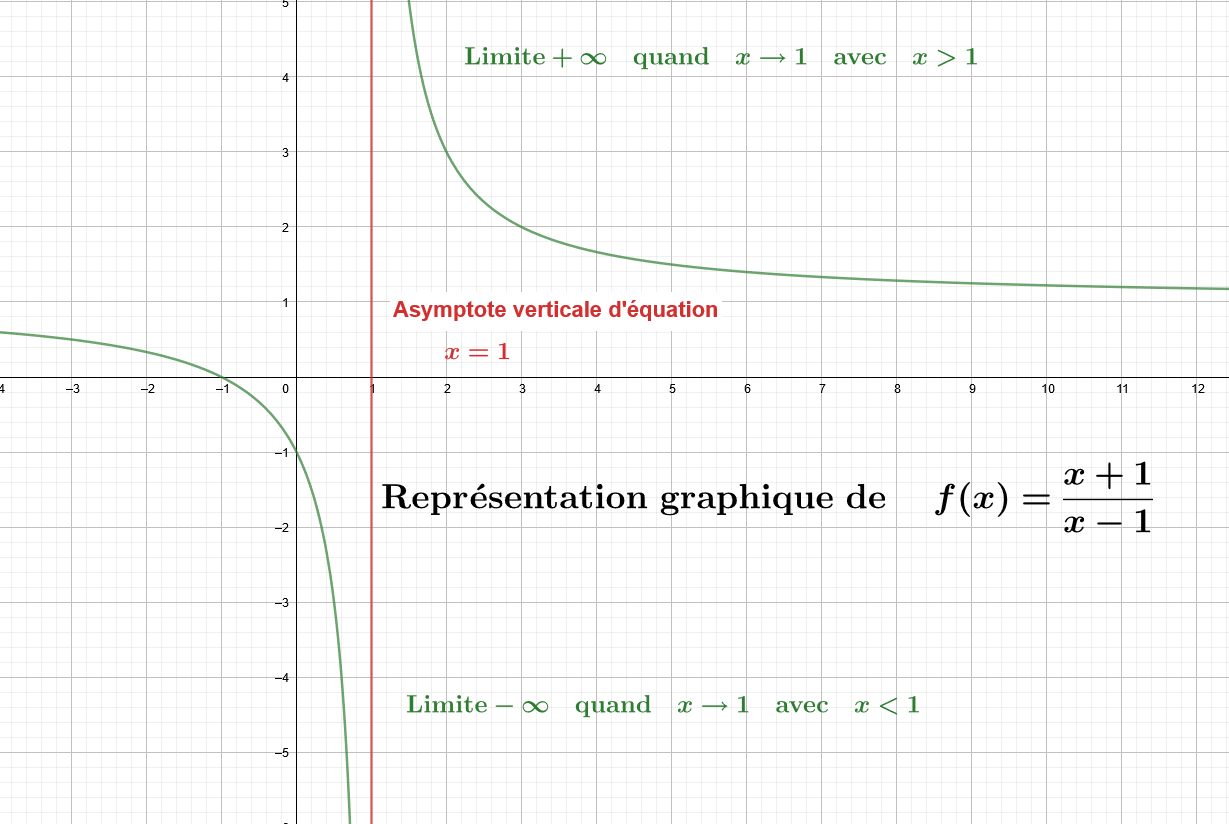
Une illustration de l'importance de ce signe est donné par le calcul de $ \lim\limits _{x \rightarrow 1} \dfrac{x+1}{x-1}$
$\quad\bullet\quad$ $\lim\limits _{x \rightarrow 1} x+1=2$ et $\lim\limits _{\substack{x \rightarrow 1 \\ x>1}} x-1=0^{+}$
donc $\lim\limits _{\substack{x \rightarrow 1 \\ x>1}} \dfrac{x+1}{x-1}=+\infty$
$\quad\bullet\quad$ $\lim\limits _{x \rightarrow 1} x+1=2$ et $\lim\limits _{\substack{x \rightarrow 1 \\ x<1}} x-1=0^{-}$
donc $\lim\limits _{\substack{x \rightarrow 1 \\ x<1}} \dfrac{x+1}{x-1}=-\infty$
La droite d'équation $x=1$ est asymptote verticale à la courbe $\mathcal{C}$.
Exemple 3 :
Déterminer la limite en $+\infty$ de $f$ définie par $f(x)=\dfrac{4 x^{2}+3}{x+2}$ sur $\left.\left.x \in\right]-2 ;+\infty\right]$
On a $\lim\limits _{x \rightarrow+\infty} 4 x^{2}+3=+\infty$ et $\lim\limits _{x \rightarrow+\infty} x+2=+\infty$
On obtient un schéma $\dfrac{\infty}{\infty}$ qui est une forme indéterminée.
Méthode :
Pour lever l'indétermination précédente, on factorise par les termes de plus au degré au numérateur et au dénominateur :
$f(x)=\dfrac{x^{2}\left(4+\dfrac{3}{x^{2}}\right)}{x\left(1+\dfrac{2}{x}\right)}=\dfrac{x\left(4+\dfrac{3}{x^{2}}\right)}{1+\dfrac{2}{x}}$
Or $\lim\limits _{x \rightarrow+\infty} 4+\dfrac{3}{x^{2}}=4$ d'où $\lim\limits _{x \rightarrow+\infty} x\left(4+\dfrac{3}{x^{2}}\right)=+\infty$
Comme $\lim\limits _{x \rightarrow+\infty} 1+\dfrac{2}{x}=1,$ on a donc $\lim\limits _{x \rightarrow+\infty} f(x)=+\infty$
A
Théorème de comparaison :
Propriété 1 :
Si $f$ et $g$ sont deux fonctions telles que :
Pour $ x $ assez grand, $f(x) \geq g(x)$ et $\lim\limits _{x \rightarrow+\infty} g(x)=+\infty$
Alors $\lim\limits _{x \rightarrow+\infty} f(x)=+\infty$
Remarque 1 :
Si pour $x$ assez grand, $f(x) \leq g(x)$ et si $\lim\limits _{x \rightarrow+\infty} g(x)=-\infty$ alors $\lim\limits _{x \rightarrow+\infty} f(x)=-\infty$
B
Théorème des gendarmes :
Propriété 1 :
Si $f, g$ et $h$ sont des fonctions et $l$ un nombre réel tel que:
$\quad\bullet\quad$ Pour $x$ assez grand, $g(x) \leq f(x) \leq h(x) $
$\quad\bullet\quad \lim\limits _{x \rightarrow+\infty} g(x)=l$ et $\lim\limits _{x \rightarrow+\infty} h(x)=l$
Alors $ \lim\limits _{x \rightarrow+\infty} f(x)=l$.
VI
Cas de la fonction exponentielle
Propriété 1 :
Limites finies de fonctions de références : $ \lim\limits _{x \rightarrow+\infty} e^{x}=+\infty \quad\quad\quad\quad \lim\limits _{x \rightarrow-\infty} e^{x}=0$
$\bullet$ Soit $h$ définie sur $\left[0 ;+\infty\left[\right.\right.$ par $h(x)=e^{x}-x$
On a pour tout $x>0, h^{\prime}(x)=e^{x}-1$
$h^{\prime}(x)>0 \iff e^{x}-1>0 \iff x>0$
On en déduit que $h$ est croissante sur $[0 ;+\infty[$.
Comme par ailleurs $h(0)=0$, on a donc pour tout $x>0, h(x) \geq 0$
c'est à dire $e^{x}-x\geq 0$ d'où : $e^{x} \geq x$
Comme $\lim\limits _{x \rightarrow+\infty} x=+\infty$ ,
par comparaison on obtient $\lim\limits _{x \rightarrow+\infty} e^{x}=+\infty$
$\bullet$ On pose $X=-x $ .
On a $\lim\limits _{x \rightarrow-\infty} e^{x}=\lim\limits _{X \rightarrow+\infty} e^{-X}=\lim\limits _{X \rightarrow+\infty} \dfrac{1}{e^{X}}$.
D'après le cas précédent, $\lim\limits _{X \rightarrow+\infty} e^{X}=+\infty$ donc $\lim\limits _{X \rightarrow+\infty} \dfrac{1}{e^{X}}=0$
Propriété 2 :
Propriété des croissances comparées :
$\quad\bullet\quad\lim\limits _{x \rightarrow+\infty} \dfrac{e^{x}}{x}=+\infty \quad\quad\quad\quad\bullet\quad \lim\limits _{x \rightarrow-\infty} x e^{x}=0 \quad\quad\quad\quad\bullet\quad \lim\limits _{x \rightarrow 0} \dfrac{e^{x}-1}{x}=1$
Remarque 1 :
Pour tout entier naturel $k$ non nul, $\lim\limits _{x \rightarrow+\infty} \dfrac{e^{x}}{x^{k}}=+\infty$ et $\lim\limits _{x \rightarrow-\infty} x^{k} e^{x}=0$
Méthode :
On retient que la fonctione exponentielle l'emporte toujours sur des fonctions polynômes.

















