Définition 1 :
On calcule la valeur d’une expression littérale lorsque l’on attribue une valeur aux lettres contenues dans l’expression.
Si une même lettre est utilisée plusieurs fois, on lui attribue le même nombre à chaque fois.
Exemple 1 :
Calculer l’expression $A = 5 \times (6 - x)+3x-7y$ lorsque $x=2$ et $y=1$ .
On n’oubliera pas de remettre le signe $\times$ à $3x$ et $7y$
$A = 5 \times (6 - x)+3 \times x-7 \times y$
$A = 5 \times \underline{(6 - 2)}+3 \times 2 -7 \times 1$
$A = \underline{5 \times 4}+3 \times 2 -7 \times 1$
$A = 20+\underline{3 \times 2} -7 \times 1$
$A = 20+6 -\underline{7 \times 1}$
$A = \underline{20+6} -7$
$A = \underline{26 -7}$
$A = 19$
III
Distributivité de la multiplication sur l'addition :
Exemple 1 :
Pour effectuer du calcul mental, on utilise souvent une astuce :
$17\times 11 = 17 \times (10 + 1) = 17 \times 10 + 17 \times 1$
On utilise la
distributivité de la multiplication sur l'addistion.
On peut faire la même chose en calcul littéral :
$ 17 \times (10 + x) = 17 \times 10 + 17 \times x=170+17 x$
On dit qu'on a
distribué 17 sur la somme de 10 et $x$.
Propriété 1 :
Formule de la distributivité :
$k \times (a+b)=k \times a+k \times b$
$k \times (a-b)=k \times a-k \times b$
Exemple 2 :
Appliquer la distributivité à :
$\begin{align}
-5 (2x + 3)&=-5 \times 2x + (-5) \times 3\\
&=-10x - 15
\end{align}$
B
Développer un produit :
Définition 1 :
Développer une expression littérale, c’est transformer un produit en somme ou différence.
Exemple 1 :
Développer $A = {4} \times (6+2x)$ C’est un produit de 4 par (6+2x)
$A = 4 \times 6+ 4 \times 2x$
$A = 24 + 8x$
C’est une somme de 24 et $8x$
Exemple 2 :
Attention à ne pas oublier la règle des signes :
Développer
$\begin{align}
A &= {-4} \times (3x-5)\\
&=(-4)\times 3x + (-4) \times (-5)\\
&=-12x + 20\\
\end{align}$
Exemple 3 :
Attention aux puissances de $x$ :
Développer
$\begin{align}
A &= {5x} \times (2-x)\\
&=(5x)\times 2 + (5x) \times (-x)\\
&=10x -5x^2\\
\end{align}$
Définition 1 :
Factoriser une expression littérale, c’est transformer une somme ou une différence en un produit,
c’est l’inverse du développement.
Exemple 1 :
$A = \textbf{5} \times x + \textbf{5} \times {3}$ On détecte le facteur commun aux deux produits
$A = {5} \times (x+{3})$ On écrit entre parenthèses les deux autres facteurs.
Exemple 2 :
Si les produits ne sont pas apparents, il faut les faire apparaître.
$B = {24} -{4}x$
$B = {4 \times 6} -{4} \times x$ On fait apparaître le facteur commun : 4
$B = {4 \times (6 -x)}$ On factorise
Définition 1 :
Réduire une somme, c’est l’écrire avec le moins de termes possibles (en regroupant les termes de même espère).
Méthode :
Pour réduire une somme, on doit factoriser.
Exemple 1 :
$\bullet\quad 4x + 5x = x(4+5)=9x$ On a factorisé par $x$
4 carottes + 5 carottes font (5+4) carottes soit 9 carottes.
$\bullet\quad B= 4x+6y+2x-y=4x+2x+6y-y=(4+2)x+(6-1)y=6x+5y$
balles + 6 torchons + 2 balles – 1 torchon = 6 balles + 5 torchons »
$\bullet\quad C= 3x+4-7x=x(3-7)+4=-4x+4$
Attention, le "+4" n'est pas factorisable par $x$. Il ne peut s'ajouter aux autres termes.
Méthode :
Réduction d'une somme
$A = {4}x+ {6}y -{7}x +{4}x^{2} - {5}y $
$A = {4}x-{7}x)+{6}y-{5}y +{4}x^{2}$
$A = {-3}x+{1}y +{4}x^{2}$
$A = {-3}x+y +{4}x^{2}$
Définition 1 :
Réduire un produit, c’est l’écrire avec le moins de facteurs possibles.
Méthode :
On procède ainsi :
1. On détermine le signe du produit
2. On calcule le produit des valeurs numériques
3. On effectue le produit des lettres.
Exemple 1 :
$A=2x\ (-3) = - 6 x$
$B=4x \times 2x = 8 x^2$
$C=-3x \times (-5)=15x$
$D=-4x\times (-2x)=8x^2$
Exemple 2 :
Réduction d'un produit
$B = {5} \times {3}x \times y \times {4}x^{2}$ Je rajoute les signes $\times$
$B = {5} \times {3}\times x \times y \times {4}\times x^{2}$ Je réordonne les facteurs, lettres à droite.
$B = {5} \times {3}\times {4} \times x \times x^{2} \times y $ Je calcule et réduis
$B =60 \times x^{3} \times y $ Je supprime les signes $\times$ qui sont devant des lettres.
$B =60 x^{3} y $
C
Le signe "-" devant une parenthèse :
Méthode :
On peut réduire un signe "-" devant une parenthèse, en supprimant la parenthèse et le signe "-", à condition de changer
tous les signes à l'intérieur de la parenthèse.
Exemple 1 :
$\begin{align}
A & = {4} – ({3}x -{5}) \\
& = {4} -{3}x + {5}
\end{align}$
Méthode :
On peut réduire un signe "-" devant une parenthèse, en ajoutant le facteur 1 et en prpocédant à la distributivité.
Exemple 2 :
$\begin{align}
A &= 2-(4x-7)\\
&= 2-1\times(4x-7)\\
&= 2-1\times 4x-1\times(-7)\\
&=2-4x+7\\
&=9-4x
\end{align}$
Comprendre :
D'où cela vient?
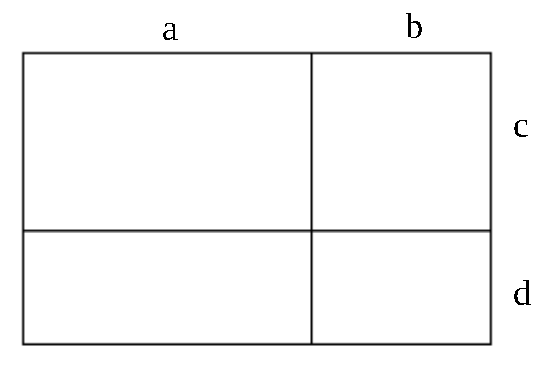
L’aire du rectangle est donnée à la fois par :
$(a+b)(c+d) $
et $a \times c+a \times d + b \times c+b \times d$ (la somme des aires de chaque rectangle)
Propriété 1 :
Double distributivité :
$(a+b)(c+d) = a \times c+a \times d + b \times c+b \times d $
Exemple 1 :
$A = ({5}x-{6})({2}x+{1})$
$A= {5}x \times {2}x+{5}x \times {1}-{6} \times {2}x-{6} \times {1}$ Je réduis les produits.
$A= {10}x^2+{5}x -{12} x-{6}$ Je réduis la somme.
$A= {10}x^2-{7} x-{6}$









